SimplicityTheory |
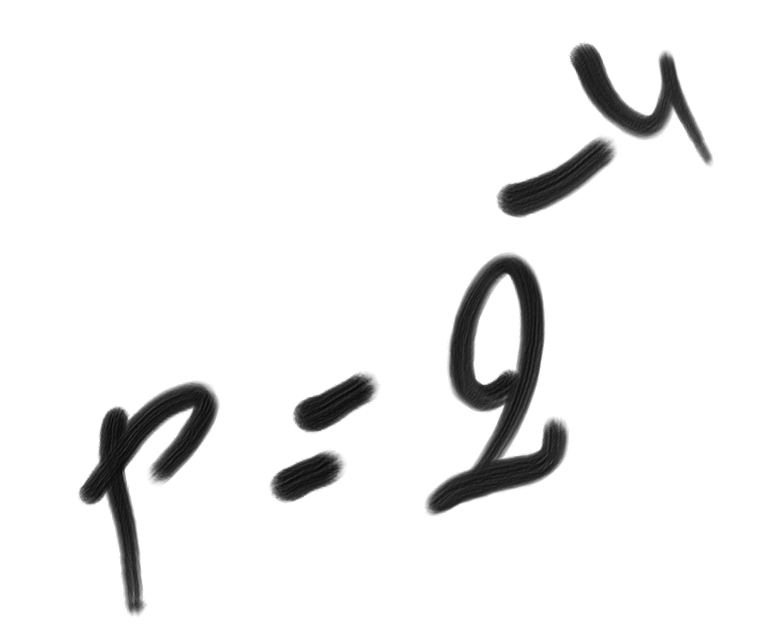 |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated January 2019)
![]()
How can an eclipse be unexpected?
Events may be anticipated and yet be unexpected! |
image: Sylvia Fidalgo
 During the early hours of September 28th, 2015, I could observe a spectacular lunar eclipse. I woke up at 4:30 to witness the event (I took a poor photo; Sylvia’s (shown here) is much better: it shows the end of the process, as the moon exits the Earth’s shadow).
During the early hours of September 28th, 2015, I could observe a spectacular lunar eclipse. I woke up at 4:30 to witness the event (I took a poor photo; Sylvia’s (shown here) is much better: it shows the end of the process, as the moon exits the Earth’s shadow).
(see also a beautiful footage of a recent solar eclipse).
According to Simplicity Theory, only an unexpected event could bring me to interrupt a well-earned sleep. How can an eclipse be unexpected? Such events are predicted centuries ahead! How can predicted events be unexpected?
Indeed, the event would have been much bigger news if it hadn’t been anticipated. Just imagine that the moon gets occulted next night! But the eclipse event lies at the other extreme. We know in advance everything there is to know about it: what will happen and when it will happen. The event is even hardly distinguishable from similar past eclipses (for the layperson). And yet it remains unexpected, at least for people like me, like Sylvia who woke up even earlier that day to take the photo, like several of my family members elsewhere in Europe or like the journalists who commented the event in the media.
This example demonstrates that ’unexpected’ should not be confused with ‘unanticipated’. By definition, unexpectedness U is the difference between generation complexity and description complexity: Cw – C.
Generation complexity Cw
In the ‘normal’ world, the full moon shines. One need specific conditions to get to a world in which the moon is shadowed by the Earth. There are two ways to compute the complexity of these conditions.
Temporal lottery
As for proximity effects, one may consider the odds that we get a lunar eclipse today. One may remember the date of the last occurrence of a similar event and consider the time elapsed since as a good estimator of the event’s ‘periodicity’. I can remember that during my holiday in Greece in summer 2008, I could see a partial lunar eclipse. My only memory of a total lunar eclipse dates back to some twenty years. This estimate may be objectively false, but it is the kind of subjective calculation people must rely on. I may therefore believe that a total lunar eclipse that is visible from where I am (which presupposes that there are no clouds) occurs once every twenty years.
If we regard the "world-machine" as a temporal lottery, my (over-)estimate of the generation complexity amounts to log2(20 × 365) = 12.8 bit.
Causal complexity
We may adopt another view of the "world-machine" in which we consider causal processes that may bring us from a ‘normal’ world into an ecliptic world. For a lunar eclipse to occur, the sun, the Earth and the moon must be perfectly aligned, in that order, at the right time for me to be on a location facing the moon. Most popular comments mentioned the perfect alignment of the sun, the Earth and the moon ("la Terre était ce lundi parfaitement alignée avec la Lune et le Soleil").
This causal estimate of generation complexity relies on one’s knowledge of this part of the solar system’s geometry and of the precision hidden in the word ‘perfectly’.
Description complexity C
The very day of the eclipse, the description complexity of the date is of course zero. The only term remaining in the description complexity comes from the conceptual complexity of the event.
The nature of the event is almost entirely captured by the concept ‘eclipse’. It is not easy to assess the complexity of a concept. A proxy can be the frequency of the word on the Web. A search on two Web search engines indicates a proportion of 579/(2 × 106) and of 14.7/106 pages containing the word ‘eclipse’. The conversion of these frequencies into complexity (the complexity of dealing with ‘eclipse’ by chance) gives C(s) = 12 bit and C(s) = 16 bit.
These are estimates of the complexity of introducing the notion of ‘eclipse’ out of the blue for normal people. If we combine our estimates for generation and description complexity, we get a zero (or even worse: negative) value for unexpectedness U. This means that normal people don’t care about eclipses because the concept of eclipse does not belong to their context or concerns, as revealed by a large value of C(s). Note however that description complexity may be significantly lower:
- for people interested in science (like myself)
- if we search only among possible events, as when looking for the news of the day
- if the notion of eclipse is already in the context
Bibliography
Cilibrasi, R. & Vitányi, P. (2007). The Google similarity distance. IEEE Transactions on Knowledge and Data Engineering, 19 (3), 370-383.
![]()