SimplicityTheory |
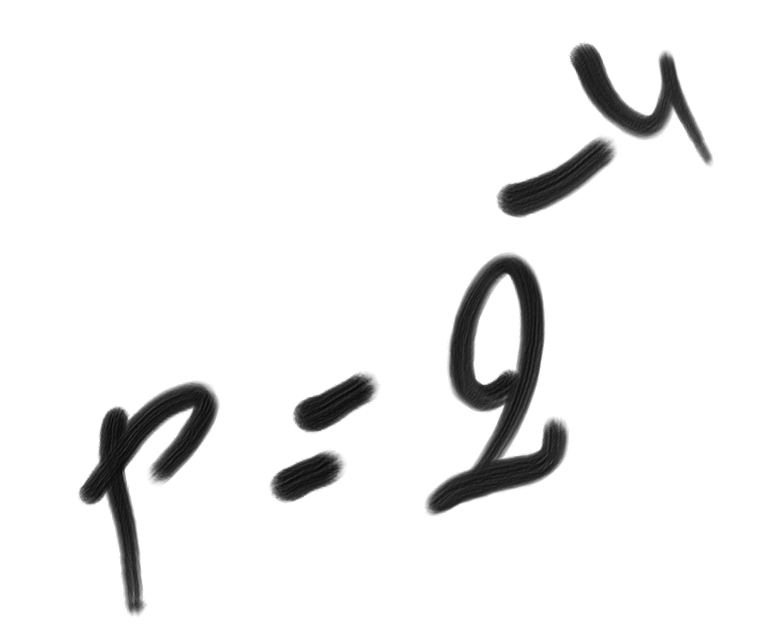 |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)
The "next door" effect (proximity)
Closer events are simpler and therefore more unexpected. |
News is a perishable product, good only when fresh. (Warren 1934/1959:15)

In November 2007, as I headed toward the Centro di Scienza Cognitiva in Torino to give a lecture about unexpectedness, I witnessed an accident between a car and a tram just one block away from via Po. I took the photo and made some impression by showing it during the talk, as I was speaking about the importance of space and time proximity.
Why are events more unexpected when they happen closer? And how much more?
By definition, unexpectedness U is the difference between generation complexity and description complexity: Cw – C.
Generation complexity Cw
Suppose you know from experience that the kind of event s you consider (e.g. an accident involving a tram) occurs with spatiotemporal density De , which means De = 1/Ve if there is one occurrence on average per spatiotemporal volume Ve.
Notes:
- You may estimate De by making Ve equal to the smallest hypervolume centred on self enclosing the closest remembered instance of s; it can be shown to be a good estimator of De. In other terms, you may retrieve from memory the latest and closest occurrence of s.
- Relevant dimensions include space and time, but also social distance. Social distance should be taken as proportional to gk where k is the distance in the acquaintance graph and g the average degree in this graph (supposing k remains small to avoid small-world effects).
Description complexity C
 When the event is close, its location requires less complexity. Let’s consider first two spatial dimensions only. Suppose locations are ranked egocentrically, by increasing distance from self. There are about
v_sub(s)) -->
\( 2 \pi d / \sqrt{v_s} \)
different locations at distance d (the approximation is good for \(d / \sqrt{v_s}\) not too small).
A location x at distance d in a two-dimension space requires no more than
\(\log_2(\pi d^2/v_s)\)
bits to be unambiguously determined:
C(x) < log2(πd2/vs)
When the event is close, its location requires less complexity. Let’s consider first two spatial dimensions only. Suppose locations are ranked egocentrically, by increasing distance from self. There are about
v_sub(s)) -->
\( 2 \pi d / \sqrt{v_s} \)
different locations at distance d (the approximation is good for \(d / \sqrt{v_s}\) not too small).
A location x at distance d in a two-dimension space requires no more than
\(\log_2(\pi d^2/v_s)\)
bits to be unambiguously determined:
C(x) < log2(πd2/vs)
More generally, if the event occurs within an ego-centred spatiotemporal volume ve, then the complexity of x amounts to: $$C(x) \le \log_2 (\frac{v_e}{v_s})$$ Finally: $$\boxed{U(x) \ge \log_2 (\frac{V_e}{v_e})}$$ This explains why close events (ve small) are more unexpected.
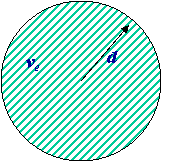 If we consider only spatial dimensions in a two-dimension space, then:
If we consider only spatial dimensions in a two-dimension space, then: U(l) > 2 × log2 (R/d)
where d is the distance to the event and R is the distance to the closest remembered occurrence.In a one-dimension space, we would have: U(x) > log2 (R/d). This accounts for recency effects.
When social distance is taken into account, U is proportional to the degree of separation in the social graph.
Bibliography
Dessalles, J.-L. (2007). Spontaneous assessment of complexity in the selection of events. Technical Report ParisTech-ENST 2007D011.
Dessalles, J-L. (2008). Coincidences and the encounter problem: A formal account. In B. C. Love, K. McRae & V. M. Sloutsky (Eds.), Proceedings of the 30th Annual Conference of the Cognitive Science Society, 2134-2139. Austin, TX: Cognitive Science Society.
Dessalles, J-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes-Science Publications.
Dimulescu, A. & Dessalles, J-L. (2009). Understanding narrative interest: Some evidence on the role of unexpectedness. In N. A. Taatgen & H. van Rijn (Eds.), Proceedings of the 31st Annual Conference of the Cognitive Science Society, 1734-1739. Amsterdam, NL: Cognitive Science Society.
Warren, C. N. (1934). Modern news reporting. New York: Harper & Brothers, ed. 1959.
![]()