SimplicityTheory |
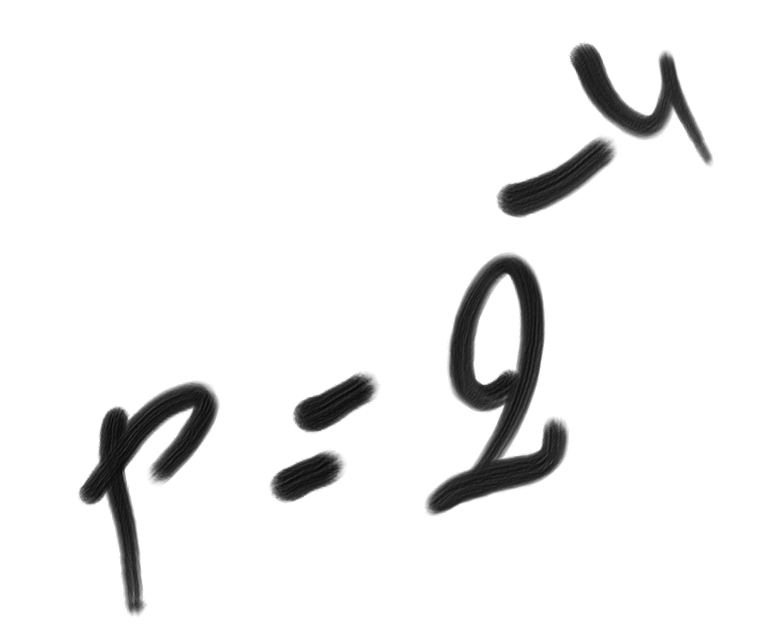 |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)
Simplicity Theory and Probability
Oddities are often more complex. This is what makes them exceptional (and therefore simple)! |


Unambiguously describing the straight tower (above, left) requires some complexity, as the tower looks like many others. We have to mention the number of stores, the presence of columns, and so on. If the tower happens to lean by a certain angle (above, right), then it seems that the complexity will be even larger, as we have now the additional burden of describing two angles: the direction of the leaning and its amount.
This impression is wrong!
Remember that complexity measures the shortest description of objects. The path to the shortest determination has now changed. If there is only one leaning tower in the country, the mention of this unique characteristics is sufficient to determine the tower in its class. Details that were necessary to determine the straight tower can now be omitted.
This contributes to making the tower interesting: being unique for a simple reason, it is unexpected.
Quiz: Find a simple shape among the ones in the figure below.

Answer: the simplest shape turns out to be the complex one! Squares have indeed a simple shape, but you still need log2(11) = 3.4 bits to discriminate them from one another. The most concise description of the odd object does not require that you describe it in every detail. You just need to mention that it is the odd one.
All human beings are unique. You are unique!![]()
Unfortunately for most of us (and there is a theorem saying that it must be so!), we are indeed unique, but for complex reasons. Some individuals’ efforts to appear in the Guiness book of records (e.g. by wearing 155 T-shirts) can be interpreted as attempts to lower their description complexity by having some unique characteristics (see the Robert Wadlow example).
Bibliography
Dessalles, J.-L. (2007). Spontaneous assessment of complexity in the selection of events. Technical Report ParisTech-ENST 2007D011.
Dessalles, J-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes-Science Publications.
Dessalles, J-L. (2008). Coincidences and the encounter problem: A formal account. In B. C. Love, K. McRae & V. M. Sloutsky (Eds.), Proceedings of the 30th Annual Conference of the Cognitive Science Society, 2134-2139. Austin, TX: Cognitive Science Society.
Dimulescu, A. & Dessalles, J-L. (2009). Understanding narrative interest: Some evidence on the role of unexpectedness. In N. A. Taatgen & H. van Rijn (Eds.), Proceedings of the 31st Annual Conference of the Cognitive Science Society, 1734-1739. Amsterdam, NL: Cognitive Science Society.
![]()