SimplicityTheory |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated April 2016)
![]()
Improbable situations are unexpected (and vice versa) |
One of ST’s main claims is that unexpectedness can be used to define ex post probability, thanks to the following formula:
p = 2–U |
This formula, proposed in 2006, suggests that human beings assess probability through complexity, not the reverse.
Note: The preceding formula is more adequate than Solomonoff’s classical definition of algorithmic probability, which amounts to p = 2–Cw. His definition takes only into account generation complexity Cw.
See Remarkable lottery drawings to get convinced.
For sure, the regular pattern on the right would be incredibly surprising if seen, say, on a for long uninhabited island (Cw large again).
If we followed Solomonoff’s definition, all real life situations would have virtually zero-probability to exist, as they would need countless parameters to be set up to have a chance to occur. This makes Solomonoff’s definition of probability of little interest for practical purposes.
By contrast, ex-post probability, as defined by p=2–U, matches human intuition and makes correct predictions. Here is an example.
Of course, this reasoning is shockingly false. We ‘feel’ that being aligned is a salient feature. Knowing that, Probability Theory could propose a probability value. Yes, but who says what is salient (or relevant) and what is not? Is the absolute orientation of the line relevant? Is the hygrometry value in the room relevant? Or the birthdate of the thrower? If the falling coins form a regular shape like a Six on a playing card ![]() , how would we know that that shape was relevant in the first place?
, how would we know that that shape was relevant in the first place?
Simplicity Theory has the answer. Relevant features are those that generate complexity drop (= compression).
Generating the falling coins event (regardless of the face) is complex: the x-y position of each coin (i.e. 12 real numbers for 6 coins, limited by some reasonable precision) must be generated independently.
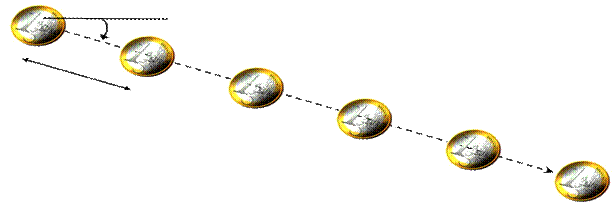
On the other hand, describing the situation is significantly simpler. It only requires 4 numbers: two numbers to determine one coin position, one number to designate the direction of the line and one more number for the spacing.
Complexity drop Cw – C amounts to 12 – 4 = 8 numbers, equivalent to 48 bits if one can discriminate 64 values for each number. This corresponds to an amazing low probability: p = 3.6 10–15, which amounts to getting 48 tails in a row while flipping a coin. If I witnessed such a marvel, I’d rather imagine a trickery to diminish generation complexity (see Remarkable lottery drawings and The running nuns).
The complexity drop rule can be used to determine which are the relevant features to observe. If there is no simple head-tail pattern among the fallen coins, just ignore them, as they won’t produce any compression. If the line is parallel to the edge of the table, notice it, as it makes the angle simple.
Suggestions: Compute the additional complexity drop due to the fact of getting 6 heads or 6 tails.
Compute complexity drop when the coins are aligned but not evenly spaced.
Saillenfest, A. & Dessalles, J-L. (2015). Some probability judgments may rely on complexity assessments. Proceedings of the 37th Annual Conference of the Cognitive Science Society, to appear. Austin, TX: Cognitive Science Society.
![]()