SimplicityTheory |
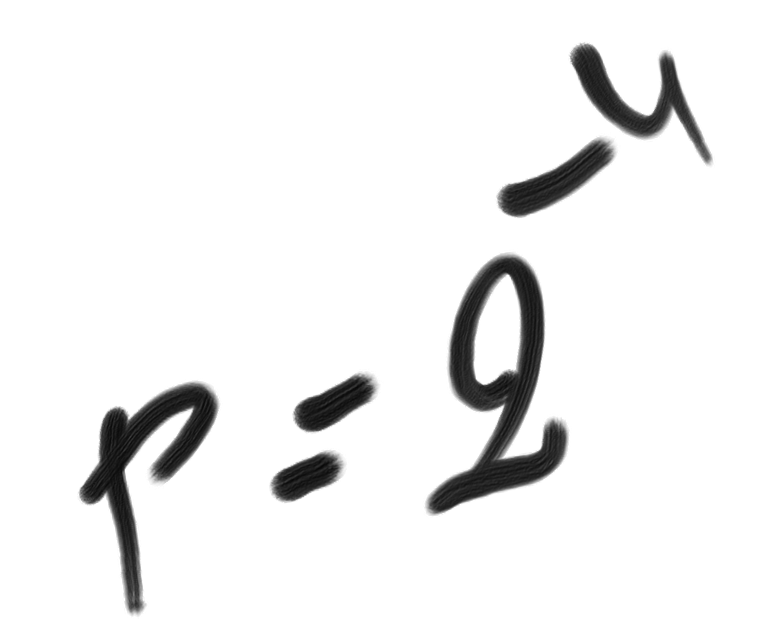 |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)
The ‘Rabid Bat’ effect (generation complexity)
The causal complexity of an event adds to its unexpectedness. |
The following comic scene (original in French; see also in video) illustrates how events that require a complex story for the "WMachine.html(world-machine)" to make them happen are considered unlikely.

|
"There is one in ten million chance of getting bitten by a rabid bat.
So, I’m not curious, but I would really like to know how the guy managed to estimate that we have ALL - on average - one chance in ten million of getting bitten. Yes, because well... Myself, I’m living in the 10th district [of Paris]. Well, first, the 10th district, where bats are concerned, it’s a quite calm place, one must admit. What’s more, I’m living five floors up without a lift, I’ll tell you, there is a digital lock at the entrance door and an entry phone. Ha, ha ! So, I’ll tell you, the bat can always turn up, you see ! So, but ok, suppose it does. A bat arrives. A rabid one. (...) So... Hop ! It starts tinkering with my code. It’s there, tinkering. It tries, it tries. (...) Pan ! It hits on the right code ! It still needs to imitate the voice of a guy I know !!! Otherwise, I won’t open ! (...) Well ! It reaches my floor ... What proves that it will knock at MY door? There’re four apartments on the floor..." © JEAN-MARIE BIGARD / PIERRE PALMADE |
By definition, unexpectedness U is the difference between generation complexity and description complexity: Cw – C. An event that is complex to generate (large Cw) will appear more unexpected. It will therefore appear more improbable, thanks to the formula p=2–U.
You may appreciate the accumulation of details aiming at increasing generation complexity Cw. The target situation (Bigard getting bitten by a rabid bat) is difficult to generate in the known world, since:
♦ there are few bats in the 10th district of Paris
Bringing one rabid bat by chance to Bigard’s building is difficult. Various computations of Cw are possible (bat-centred or building-centred). They all end up with: Cw = log2 B1 – log2 B2 + constant, where B1 and B2 represent the number of buildings and the number of bats in the 10th district. Note that the ‘constant’ includes the logarithm of the proportion of rabid bats in the bat population. Note also that the mention of the 10th district (a homogeneous, densely populated district) aims at increasing the difference log2 B1 – log2 B2 (but it is "paid" on the complexity side, C; therefore, the authors do not mention "I am living in the south-west part of the 10th district").
♦ there are many combinations for the digital lock
Finding the right combination by chance amounts to log2 C1, where C1 is the number of combinations.
♦ it is difficult for a bat to imitate the voice of one of Bigard’s friends
Here, there are two sources of high generation complexity: the rabid bad is not supposed to know Bigard’s friends (hence a term in log2 V1 where V1 is the total number of recognizable voices); and even in the alternative reality that is already installed, bats are not supposed to be very good at imitating human voices.
♦ there are four apartments on the floor
This adds two bits to Cw.
We could push the analysis even further (why the 10th district and not the 1st one?; why mentioning the absence of lift...). The point is that in the absence of a model of how the world works (e.g. that climbing stairs is tiring, therefore higher motivation is required to climb further up...), there is no chance to understand the funny aspects of the story. Conversely, any proper assessment of Cw is sufficient here to understand why the event (Bigard getting bitten by a rabid bat) is highly improbable.
Moreover, the difference Cw - C provides a strict relevance criterion for the story. For instance, Bigard does not mention that the entrance door is blue, as it would have no bearing on Cw and would unnecessarily increase C.
Bibliography
Dessalles, J-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes-Science Publications.
Dessalles, J-L. (2013). Algorithmic simplicity and relevance. In D. L. Dowe (Ed.), Algorithmic probability and friends - LNAI 7070, 119-130. Berlin, D: Springer Verlag.
![]()